
Учебник «Математика 1 класс» авторов Моро — это современное пособие, предназначенное для обучения детей основам математики в первом классе. Он соответствует федеральным государственным образовательным стандартам и содержит все необходимые темы для успешного освоения школьной программы.
ГДЗ по Математике 4 Класс Часть 1 Страница 64 Моро, Волкова, Степанова — Подробные Ответы
Начерти отрезок длиной 60 мм. Узнай, сколько миллиметров в пяти шестых долях этого отрезка.

1) 60 : 6 = 10 (мм) — одна шестая доля этого отрезка.
2) 10 * 5 = 50 (мм)
Ответ: 50 мм в пяти шестых долях этого отрезка.
Начерти такой прямоугольник. Вырежи его и разрежь по проведённому в нём отрезку. Проверь наложением, что полученные треугольники равны. Найди площадь одного треугольника.


Площадь прямоугольника: 3 ∙ 5 = 15 см2 = 1500 мм2
Площадь треугольника: 1500 : 2 = 750 мм2
За 7 дней в столовой израсходовали 21 кг масла. На сколько дней при той же норме расхода хватит 36 кг масла? На сколько дней хватило бы этого масла, если бы каждый день расходовали на 1 кг больше?
21 : 7 = 3 (кг) — расход масла в день.
36 : 3 = 12 (дней) — сколько хватит масла при таком расходе.
3 + 1 = 4 (кг) — новый ежедневный расход.
36 : 4 = 9 (дней) — сколько хватит масла при увеличенном расходе.
Ответ: 36 кг масла хватит на 12 дней при прежнем расходе и на 9 дней при увеличенном.



Сравни уравнения каждой пары и их решения.
На сколько равных частей разделён каждый квадрат на чертеже? Найди площадь одной доли в каждом квадрате. Сравни площади этих долей.

Квадраты разделены на 4 равные части.
Площадь каждого квадрата: 2 × 2 = 4 см².
Площадь одной части квадрата: 4 : 4 = 1 см².
Площади всех частей равны, так как квадрат делится на 4 одинаковые части, и при этом общая площадь квадрата остаётся неизменной.
Ребус.




.jpg)

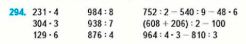





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!