
Учебник «Математика 4 класс. Часть 2» под редакцией Моро предназначен для учащихся 4 класса и является продолжением первой части. Он разработан в соответствии с федеральными образовательными стандартами и направлен на углубление знаний по математике.
ГДЗ по Математике 4 Класс Часть 2 Страница 66 Моро, Волкова, Степанова — Подробные Ответы
Реши задачи и сравни их решения.
1) Длина водохранилища 600 км, а его ширина 400 км. Поездка на катере через водохранилище по его длине занимает на 10 ч больше, чем по ширине. За сколько времени при одинаковой скорости можно пересечь водохранилище по его длине и по ширине?
2) Длина водохранилища на 200 км больше его ширины. Поездка на катере с одинаковой скоростью через водохранилище по его длине занимает 30 ч, а по ширине – 20 ч. Найди длину и ширину этого водохранилища.
Задача 1:
.jpg)
1) 600 − 400 = 200 (км) – расстояние, которое проходит катер за 10 ч.
2) 200 : 10 = 20 (км/ч) – скорость катера.
3) 600 : 20 = 30 (ч) – время поездки по длине водохранилища.4) 400 : 20 = 20 (ч) – время поездки по ширине водохранилища.
Ответ: время поездки по длине водохранилища составляет 30 ч и время движения по ширине водохранилища составляет 20 ч.
Задача 2:
.jpg)
1) 30 − 20 = 10 (ч) – время, за которое катер проходит расстояние в 200 км.
2) 200 : 10 = 20 (км/ч) – скорость катера.
3) 20 ∙ 30 = 600 (км) – длина водохранилища.
4) 20 ∙ 20 = 400 (км) – ширина водохранилища.
Ответ: длина водохранилища составляет 600 км и ширина водохранилища составляет 400 км.
Сравнение задач и их решений.Эти задачи обратные. Рассмотрим решения задач. И в первой и во второй задаче сначала мы находили скорость катера, но в первой для этого мы искали неизвестное расстояние, которое проходят за 10 часов, а во второй – время, необходимое для прохождения расстояния в 200 км.Затем искали нужное значение по вопросу задачи: в первой — время поездок по длине и ширине катера искали через деление: расстояние делили на найденную скорость, а во второй – длину и ширину водохранилища искали через умножение данных временных величин и найденной скорости.
В питомнике вырастили саженцы деревьев: елей было 360, а на каждый 8 елей приходилось 18 клёнов и 16 лип. Сколько всего елей, клёнов и лип вырастили в питомнике?

1) 360 : 8 = 45 (р.) – по 8 елей содержится в питомнике.
2) 18 ∙ 45 = 810 (шт.) – клёнов.
3) 45 ∙ 16 = 720 (шт.) – лип.
4) 360 + 810 + 720 = 1890 (шт.) – деревьев, в питомнике.
Ответ: 1890 деревьев всего вырастили в питомнике.
2 ц 50 кг × 4 = 250 ц × 4 = 1000 кг = 10 ц = 1 т
125 м × 8 = 1000 м = 1 км
1 м 20 см × 6 = 120 см × 6 = 720 см = 7 м 20 см
1 м 20 см ÷ 6 = 120 см ÷ 6 = 20 см
2 мин 30 с × 5 = 150 с × 5 = 750 с = 12 мин 30 с
2 ч 30 мин ÷ 5 = 150 мин ÷ 5 = 30 мин
Запиши неравенства и объясни, почему они верны.
1) Сумма чисел 289 и 1 больше их произведения.
2) Сумма чисел 289 и 0 больше их произведения.
3) Частное чисел 289 и 1 больше их разности.
1) 289 + 1 > 289 ∙ 1 − неравенство верно, так как когда мы прибавляем к числу 1, мы получаем число, большее на 1, а когда умножаем на 1, получаем число равное данному.
2) 289 + 0 > 289 ∙ 0 − неравенство верно, так как когда мы прибавляем к числу 0, мы получаем число, равное данному, а когда умножаем на 0, получаем 0.
3) 289 : 1 > 289 − 1 − неравенство верно, так как когда мы делим число на 1, то получаем число, равное данному, а когда вычитаем 1,получаем число, меньше данного на 1.
Реши те уравнения, в которых неизвестное находят умножением.
х : 100 = 90
х — неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 100 ∙ 90
х = 9000
1200 : х = 60
х — неизвестный делитель.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Решается делением.
Не подходит.
30 ∙ х = 1800
х — неизвестный множитель.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
Решается делением.
Не подходит.
х : 18 = 30
х — неизвестное делимое.
Чтобы найти неизвестное делимое, нужно делитель умножить на частное.
Решается умножением.
Подходит.
х = 30 ∙ 18
х = 540
Докажи, что в каждой окружности все диаметры делятся центром окружности на 2 равных отрезка.

Диаметр — это отрезок, который проходит через центр окружности и ограничен двумя точками на окружности. Этот центр окружности делит диаметр на два равных радиуса. Поскольку все радиусы окружности одинаковы, все диаметры делятся центром окружности на два равных отрезка.
Зеленые отрезки ОА, ОС, ОВ, OD равны по длине, так как являются радиусами одной окружности.
Красные отрезки ОК, ОМ, ОР, ОL также равны между собой, так как являются радиусами другой окружности.
Школьная хоккейная площадка длиной 50 м и шириной 20 м обнесена бортиком прямоугольной формы высотой 1 м. Сколько краски потребуется для окраски бортика с внешней и внутренней сторон, если расход краски на 1 м² составляет 140 г и краска должна быть нанесена в 2 слоя?

1) 50 ∙ 1 = 50 (м²) – площадь длинного бортика хоккейной площадки.
2) 20 ∙ 1 = 20 (м²) – площадь короткого бортика хоккейной площадки.
3) (50 + 20) ∙ 2 = 140 (м²) – площадь всех бортиков с одной стороны.
4) 140 ∙ 2 = 280 (м²) – площадь всех бортиков с двух сторон.
5) 280 ∙ 140 = 39200 (г) – расход краски, нужно для покраски бортиков в 1 слой.
6) 39200 ∙ 2 = 78400 (г) – краски нужно для покраски всех бортиков с двух сторон.
Ответ: 78400 грамм краски или 78 кг 400 грамм нужно для покраски всех бортиков с двух сторон.
Вычисли.
Ребус.





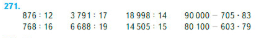

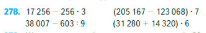






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!